GSO 2.0

The original GNU Superoptimizer (GSO) was pioneering, but has some limitations: it only handles arithmetic instructions, delivers a single result, generates impossible sequences, only supports a carry flag and has a very simple cost model.  Its big advantage is that it is fast.

Since GSO was created in 1991, there have been many advances in superoptimization.  Rather than being a single program, GSO 2.0 is a tool kit, allowing multiple approaches to be used.

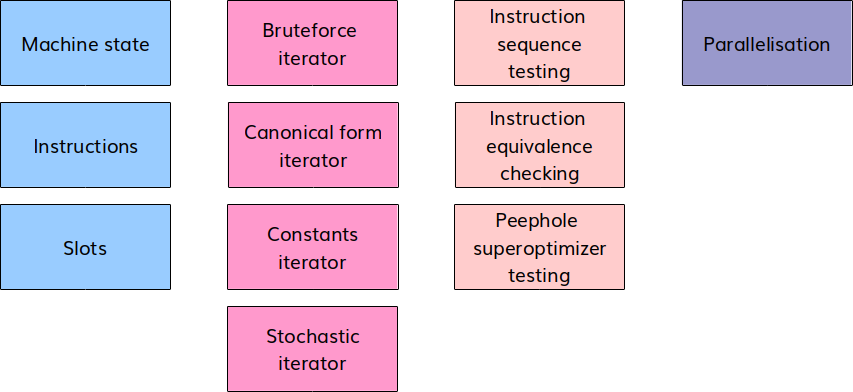
The configurability is in four categories, machine architecture, iteration approach, testing approach and parallelisation

Machine Architecture

The machine state describes what the instructions can access

• registers
• flags
• memory

The instructions are the operations that the processor can perform.  This is the “simulation” aspect of the superoptimizer and can possibly be automatically generated from tools such as CGEN

The slots describe what the superoptimizer can change in a sequence, for example slots containing registers

add r0, r1

or a slot containing constants

add r0, #128

Here is an example for the x86 architecture.

x86_Machine mach;

...

// add ax, bx
Instruction *add = new x86_add();

vector<Slot*> slots = add->getSlots();

slots[0]->setValue(0);
slots[1]->setValue(1);

add->execute(&mach, slots);

Approach to Iteration

There are a number of approaches to iteration supported.

Brute Force Iteration

This is the original approach, where the superoptimizer iterates over a sequence of items, visiting every combination

vector values = {0,1,2,3};
vector<vector::iterator> indices;

indices.push_back(values.begin());
indices.push_back(values.begin());

do {
     ...
} while(bruteforceIterate(values, indices));

Canonical Form Iteration

Iteration is optimized by ensuring that each register renaming gets tested only once when iterating over register slots

vector<Slot*> slots;
...
canonicalIterator c_iter(slots);

do {
     ...
} while(c_iter.next());

Constants Iteration

Iteration over constant slots is optimized by only testing the most frequently used constants.

vector<Slot*> slots;
...
constantIterator cn_iter(slots);

do {
     ...
} while(cn_iter.next());

Stochastic Iteration

Other approaches to iteration are possible. The stochastic iterator allows for directed exploration of the search space, similar to that provided in STOKE.

Testing

Central to superoptimization is testing whether a valid sequence has been found.

Instruction Sequence Testing

This approach checks for equivalent behavior of a sequence of instructions. This may be:

• equivalence to another sequence of instructions; or
• equivalence to an arbitrary function (as in the original GSO).

The testing is carried out by executing the sequence, with support for multiple tests to provide probabilistic correctness. For example

vector<Instruction*> insns, goal_insns;
vector<Slots*> slots, goal_slots;
... set up the above variables ...
bool success = testEquivalence(
                   insns, slots, 
                   goal_insns, slots);

Instruction Equivalence Checking

With this approach, we verify that the instructions are equivalent for all possible inputs.  The approach is two step:

• translate to SMT form; and
• call an external solver.

This approach guarantees correctness, but is expensive.  Instruction sequence testing should first be used for quick exclusion.

Peephole Superoptimizer Testing

When using superoptimization to create a peephole optimization pass for a compiler, it is useful to be able to test a large number of sequences simultaneously.  this allows us to find many equivalent sequences at once, and these sequences form new peephole optimizations.  The approach is described in a 2006 paper by Sorav Bansal and Alex Aiken.

Parallelisation

Brute force superoptimization is an embarrassingly parallel problem.  GSO 2.0 is designed to take advantage of this on multiprocessor machines.  It uses a generic master-slave MPI-based work queue.

• The master distributes work items.
• Each slave requests a work item, sending a message back if it was successful.

This is an example of the master code:

vector<vector> instruction_ids =     {{0, 1, 2}, 
    {0, 1, 2}, 
    {0, 1, 2}};
...
distributeTasks(instruction_ids);

This is an example of the slave code:

vector insn_ids;

while(getWork(insn_ids)) {
    ...
    // computation with insn_ids
    ...
}
{0, 0, 0}
{0, 0, 1}
{0, 0, 2}
{0, 2, 0}
...

Using GSO 2.0

GSO 2.0 is a work in progress. The first version was presented at the GNU Tools Cauldron in 2015.  The current code base can be found on Embecosm GitHub.  We welcome contributions from other developers.